Delta-X: Island and Secondary Channel Model, MRD, LA, USA, 2022

This dataset includes model code and output for a model that simulates changes in islands and small water channels of river delta systems in response to dynamics of sediment deposit, erosion, and changing water levels. Simulations demonstrate developmental cycles of secondary channels and how sediment dynamics can allow islands to build land vertically to keep pace with rising sea levels rather than passively drowning. The model was applied to the Mississippi River Delta as part of NASA's Delta-X project. Simulations were run for other river deltas, including the Amazon, Brahmputra, Danube, Magdalena, Nile, Orinoco, Parana, Rhine-Meuse, and Rhone rivers. The model code is provided in text format for MATLAB software. Files demonstrating initial model conditions and outputs are provided in binary MATLAB as well as NetCDF version 4 format.

There are 29 data files with this dataset. This includes one text file (.m) holding MATLAB model code, and 14 files in binary MATLAB format (.mat) accompanied by 14 files holding the same information in NetCDF version 4 format (.nc4)`.

This dataset includes model code and output for a model that simulates changes in islands and small water channels of river delta systems in response to dynamics of sediment deposit, erosion, and changing water levels. Simulations demonstrate developmental cycles of secondary channels and how sediment dynamics can allow islands to build land vertically to keep pace with rising sea levels rather than passively drowning. The model was applied to the Mississippi River Delta as part of NASA’s Delta-X project. Simulations were run for other river deltas, including the Amazon, Brahmputra, Danube, Magdalena, Nile, Orinoco, Parana, Rhine-Meuse, and Rhone rivers. The model code is provided in text format for MATLAB software. Files demonstrating initial model conditions and outputs are provided in binary MATLAB as well as NetCDF format.

Project: Delta-X

The Delta-X mission is a 5-year NASA Earth Venture Suborbital-3 mission to study the Mississippi River Delta in the United States, which is growing and sinking in different areas. River deltas and their wetlands are drowning as a result of sea level rise and reduced sediment inputs. The Delta-X mission will determine which parts will survive and continue to grow, and which parts will be lost. Delta-X begins with airborne and in situ data acquisition and carries through data analysis, model integration, and validation to predict the extent and spatial patterns of future deltaic land loss or gain.

Related publication:

Salter, G. and M. Lamb. 2022. Autocyclic secondary channels stabilize deltaic islands undergoing relative sea level rise. Geophysical Research Letters, e2022GL098885. https://doi.org/10.1029/2022GL098885

Acknowledgements:

This project received support from NASA's Earth Venture Suborbital-3 Program (grant NNH17ZDA001N-EVS3).

Spatial Coverage: This model's structure and simulation outputs are not georeferenced. Input parameters for simulations were based on characteristics of the Mississippi, Amazon, Brahmputra, Danube, Magdalena, Nile, Orinoco, Parana, Rhine-Meuse, and Rhone river deltas.

Spatial Resolution: 1 m

Temporal coverage: No fixed dates

Temporal resolution: 1 second for model operations, 1 year for saved outputs

Data File Information:

There are 29 data files with this dataset. This includes one text file holding MATLAB model code (.m), and 14 files in binary MATLAB format accompanied by 14 files holding the same information in NetCDF-4 format.

Simulation files include input parameters and values of output variables. Files containing the same information are provided in binary MATLAB (.mat) and open-source NetCDF-4 (.nc4) formats.

Table 1. File names and descriptions.

File name	Description
island_model_archive.m	Model code for MATLAB software in text format
initial_condition_island_archive.<ext>	Example simulation illustrating how initial conditions can be specified. <ext> is either “mat” or “nc4”.
<river>_simulation.<ext>	Simulations using input parameters derived from characteristics of 9 river deltas <river>: Mississippi, Amazon, Brahmputra, Danube, Magdalena, Nile, Orinoco, Parana, Rhine-Meuse, and Rhone.
mississippi_simulation.<ext>	Simulation that corresponds to results in Table S1 in the Supporting Information of Salter and Lamb (2022). The nondimensional domain length (L_star), which represents island size, is set to 19.6596.
mississippi_fig3_simulation.<ext>	Simulation that corresponds to Figure 2 below (and Figure 3 in Salter and Lamb, 2022). L_star = 20.0.
mississippi_fig4_SLR2.<ext>	Simulation that corresponds to Figure 4 in Salter and Lamb (2022). L_star = 20.0 with a doubled rate of relative sea level rise.
mississippi_fig4_SLR5.<ext>	Simulation that corresponds to Figure 4 in Salter and Lamb (2022). L_star = 20.0 with 5 times the base rate of relative sea level rise.

Table 2. Variables and descriptions.

Variable	Units	Description
Primary model outputs
x	m	vector of x coordinate values (m) measuring distance from main channel
t_save	s	vector of output times (s)
c_save	1	matrix of depth-averaged concentration values, rows correspond to t_save and columns to x
cf_save	1	matrix of friction coefficient
E_save	1	matrix of entrainment
eta_save	m	matrix of bed elevations (m)
h_save	m	matrix of water depth (m)
q_save	m2 s-1	vector of incoming water discharge per unit width (m2/s)
sea_save	m	vector of downstream water level (m)
Full parameters and variables list
B_channel	m	width of main channel, used in initial input values calculations
b_star	1	dimensionless height from bed used in main channel rouse calculation
c	1	vector of concentration values at each location corresponding to x
C1, C2	1	parameters in settling velocity formula
c_b	1	vector of near bed sediment concentration
cf	1	vector of friction coefficients
cf_channel	1	main channel friction coefficient
cf_edge	1	friction coefficient vector at cell edges
cf_island	1	scalar value of friction coefficient used in the island
cmean_method	1	switch to include vertical velocity profile in main channel near-bed concentration calculation (value=2 is default) or not included (value=1)
concentration_factor	1	parameter multiplying main channel near-bed concentration
cvert	1	vertical concentration profile in main channel, corresponding to z_up
deta	m	vector of bed elevation change within a timestep (m)
deta_thresh	m	parameter used in regulating maximum time step (m)
ds	m	grain size (m)
ds_factor	1	factor multiplying originally specified grain size
dt	s	time step (s)
dt_initial	s	initial time step (s)
dt_save	m	vector of time step duration at times corresponding to t_save
dx_edge	m	grid size (m) used to define x vector
E	1	vector of entrainment
eta	m	vector of bed elevation (m)
eta_star	1	eta non-dimensional, by main channel depth
exner_prefactor	1	rate of elevation change scaled by this to simulate nourishment width effect
g	m s-2	gravitational acceleration (m/s2)
h	m	vector of flow depth over island (m)
h_critical	m	Froude critical flow depth for reference (m)
H_diff	m	difference in water levels between two boundaries (m)
H_guess, H_guess0, H_guess1	1	values of main channel water level used in iteration procedure
H_M	m	main channel flow depth (m)
H_main	m	main channel water surface elevation (m)
h_normal	m	normal flow depth corresponding to q and S for reference (m)
H_sea	m	downstream water surface elevation, i.e. sea level (m)
ks	m	vector of roughness length (m)
ksM	m	roughness length in main channel (m)
L	m	domain length (i.e. island size or island half-width) (m)
L_star	1	L, nondimensional, by main channel depth H_M
lambda	1	bed porosity
momentum_fix	1	switch to include head loss due to momentum (included by default =1)
N	1	length of x vector, i.e. number of grid cells
q	m2 s-1	incoming discharge per unit width over the island (m2/s)
Q_channel	m3 s-1	main channel discharge (m3/s)
q_guess, q_guess0, q_guess1	m2 s-1	discharge values used in iteration (m2/s)
q_loglaw	1	discharge per unit width obtained by integrating vertical profile in main channel concentration calculations
qs_channel	m2 s-1	main channel sediment discharge per unit width (m2/s)
r	1	stretching factor for grid, default=1
R	1	sediment submerged density
r_multiplier	1	r0 factor, i.e. ratio of near-bed to depth-averaged concentration over island
r_ratio	1	vector of r_multiplier values
Re_p	1	particle Reynolds number
rho	kg m-3	water density (kg/m3)
S	1	island bed slope
S_factor	1	factor multiplying overall island water surface slope
S_island	1	water surface slope across the entire island
saveinterval	1	interval for saving model outputs (number of timesteps)
SLR	m y-1	sea level rise rate in m/yr
SLR_factor	1	factor multiplying the base rate of sea level rise
stretch	1	for setting up a stretched grid
tau_star	1	vector of shields stress over the island
tausc	1	critical shields stress
threshold_factor	1	factor multiplying critical shields stress
timesteps	1	number of time steps in simulation
timeyear	1	number of seconds in a year
u_starM	1	main channel shear velocity (m/s)
variable_chezy	1	calculate spatially variable chezy coefficient (1), or use constant value (0=default)
viscosity	m2 s-1	water kinematic viscosity (m2/s)
w_s	m s-1	particle settling velocity (m/s)
watlev_accuracy	m	accuracy for iteration of discharge/water level at island entrance (m)
q_star	1	dimensionless version of q_save (see end of code)
t	s	full vector of model times (for each time step, not just output times) (s)
t_star	1	dimensionless version of t_save, see end of code
x_star	1	x nondimensional by domain length L
z	m	z coordinate used in initial calculations to determine main channel near-bed concentration (m)
z_up	m	z coordinate in main channel from island elevation at inlet to water surface (m)

This is a one dimensional model of an island secondary channel dynamics and sediment deposition. The model shows that islands can potentially keep pace with relative sea level rise through cycles of secondary channel incision and growth followed by secondary channel deposition and annealing.

A sensitivity analysis was performed by exploring the effects of relative sea level rise and input parameters based on islands and channels of the Mississippi, Amazon, Brahmputra, Danube, Magdalena, Nile, Orinoco, Parana, Rhine-Meuse, and Rhone river deltas (Salter and Lamb, 2022)

River deltas are low-lying coastal landscapes, making them vulnerable to sea level rise. Deltas are commonly composed of islands separated by river channels. These islands are formed and maintained by sediment supply delivered from the surrounding river channels. Here, this numerical model can explain how sediment is delivered to islands, and how this sediment allows islands to build land vertically, potentially allowing them to keep pace with rising sea level rather than passively drowning. Small channels can deliver sediment from river channels to island interiors, allowing islands to keep pace with sea level. The model predicts that these small channels undergo natural cycles of deepening and shallowing, consistent with observations. Additionally, the model predicts that large islands are eventually split by larger permanent river channels, whereas small islands tend to merge, potentially explaining the range of island sizes found in river deltas. Overall, the model shows that deltaic islands undergoing sea level rise do not passively drown, but rather activate secondary channels and change their size to allow vertical land building to keep pace with sea level.

This model is one dimensional. It tracks changes in surface elevation changes along a single axis (x) from the island edge (boundary with primary water channel) and levee toward the island interior. It simulates the development of secondary channels flowing through the island and associated dynamics of sediment deposition and erosion (Figure 2). The model and its output are not georeferenced. Input parameters such as island size, water levels, discharge rates, and sediment concentrations can be adjusted to resemble a variety of real-world river delta systems.

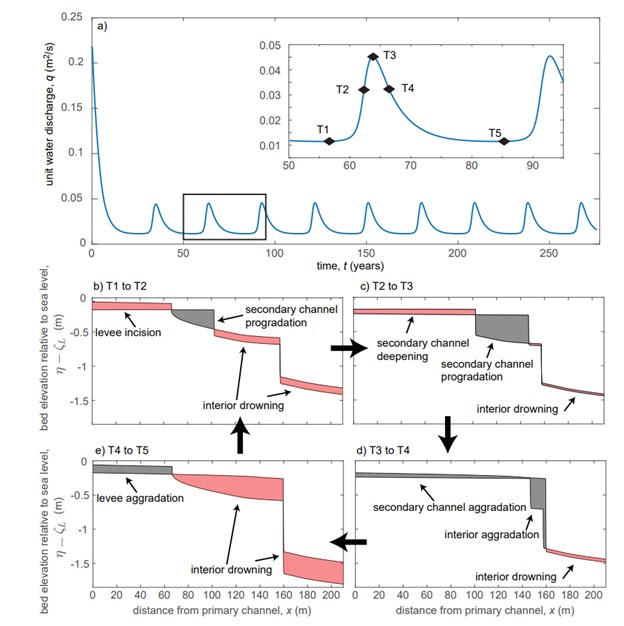
Figure 2. Examples of model behavior. [a] Time series of unit water discharge (q) for the oscillating regime. [b-e] Oscillating regime bed elevation profiles referenced to sea level (η(x) − ζL) at times indicated in the subfigure [a] inset. Red shaded regions indicate a decrease in bed elevation relative to sea level due to drowning and/or erosion; gray shaded regions indicate an increase in relative bed elevation. Source: Salter and Lamb (2022)

The model structure is explained in Salter and Lamb (2022). The user should also refer to the Supplemental Information provided with this article.

Model input parameters are specified in the MATLAB code (.m) itself. The model can be run with specified initial conditions if the hotstart parameter is set to 1 and the variables are loaded (see example initial_condition_island_archive.mat). Otherwise, the model will generate initial conditions automatically if hotstart=0. In addition, simulations using parameters based on nine river deltas are provided.

The model code is also available at https://github.com/salterg/island_secondary_channel

Salter, G. and M. Lamb. 2022. Autocyclic secondary channels stabilize deltaic islands undergoing relative sea level rise. Geophysical Research Letters, e2022GL098885. https://doi.org/10.1029/2022GL098885